Calculating Percentages
HOW TO TEACH PERCENTAGE
We often confuse students by demanding they give "110%" effort, which is, of course, impossible. No one can give 110 of something that only consists of 100 parts. A basic understanding of percentage is that it is some smaller part of a larger whole. Therefore, the percentage will always be less than the total amount.
One way to show this clearly is by relating percentage to a fraction and a decimal. The expression 25% means 25 out of 100. We can show this as 25/100 or even 0.25.

PERCENTAGES AS DECIMALS
Familiarize students with this relationship by having them use a simple calculator to convert percentages to decimals. Select a percent, such as 94%, and have them enter 94 ÷ 100 = into their calculator. Their answer will be 0.94. Do this several times and they will no longer need a calculator to "see" percentages as decimals. As you teach this simple step, be sure to practice single-digit percentages. Explain to students that 7% is 0.07, not 0.7.

MULTIPLYING BY NUMBERS LESS THAN 1
Another foundational understanding to calculating percentages is that multiplication can lead to products that are larger or smaller than the original factor.
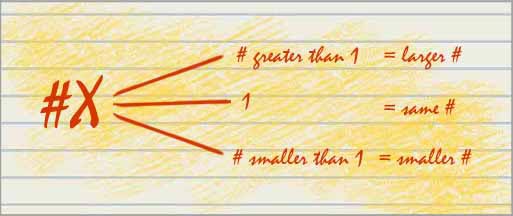
Because a percentage is less than one whole, it will be a number that is less than the original amount. Consider the purchase of a $10 t-shirt. If it is on sale for 25% off, the amount off has to be less than $10. When 10 is multiplied by a number less than 1 (in this case 0.25), it results in a smaller number (2.5 or $2.50)

Dollar amounts are a great way to begin teaching percentages, because our money is based on units of 100, just like percentages! In the t-shirt example above, 25% off means 25 out of every 100¢ is taken off. Since there are ten of these 100¢ units in the price of the t-shirt, the customer will save 25¢ ten times.
One word of caution in teaching percentage off: figuring out percentage is usually not the final step in solving the problem. In this example, the percentage ends up being $2.50, but the solution to the problem is likely the new cost of the t-shirt. Therefore, students must calculate the original price ($10) minus the percentage discounted ($2.50) to come up with the final cost of $7.50. Teachers can avoid this extra step by asking "How much will a customer save?" instead of "What is the final cost?"